最近几年算力飞速发展，很多领域进步的核心动力离不开算力。传统计算在面对日益增长的算力计算时，还是非常局限性不够用的。但我们的北京大学人工智能研究院孙仲研究员团队联合集成电路学院研究团队，成功研制出基于阻变存储器的高精度、可扩展模拟矩阵计算芯片，相关论文于2025年10月13日刊发于《自然·电子学》期刊，详细论文有兴趣的可以去看看。真的是核弹级的突破。

一、传统计算天花板，GPU硬件摩尔定律极限

矩阵方程求解作为线性代数的核心内容，在信号处理、科学计算及神经网络二阶训练等众多关键领域有着极为广泛的应用。以常规矩阵乘法相比，矩阵求逆操作对输入误差极为敏感，这就对计算精度提出了近乎严苛的要求。所以时间复杂度可达立方级。随着各种大模型对算力的需求指数级增长，传统的计算算法已经无法满足需求。

现在更为棘手的是，传统GPU硬件尺寸缩放已逼近物理极限，传统冯·诺依曼架构也面临着“内存墙”瓶颈的双重困境。数据在内存与处理器之间的频繁传输，不仅能耗大幅增加，还严重限制了计算速度。模拟计算凭借其通过物理定律直接实现高并行、低延时、低功耗运算的先天优势，重新进入了研究者的视野。传统模拟计算也并非完美无缺，低精度和难扩展等固有缺点，使其逐渐被高精度、可编程的数字计算所取代，成为了教科书中描述的“老旧技术”。

二、创新架构：多维度协同构建高精度可扩展求解器

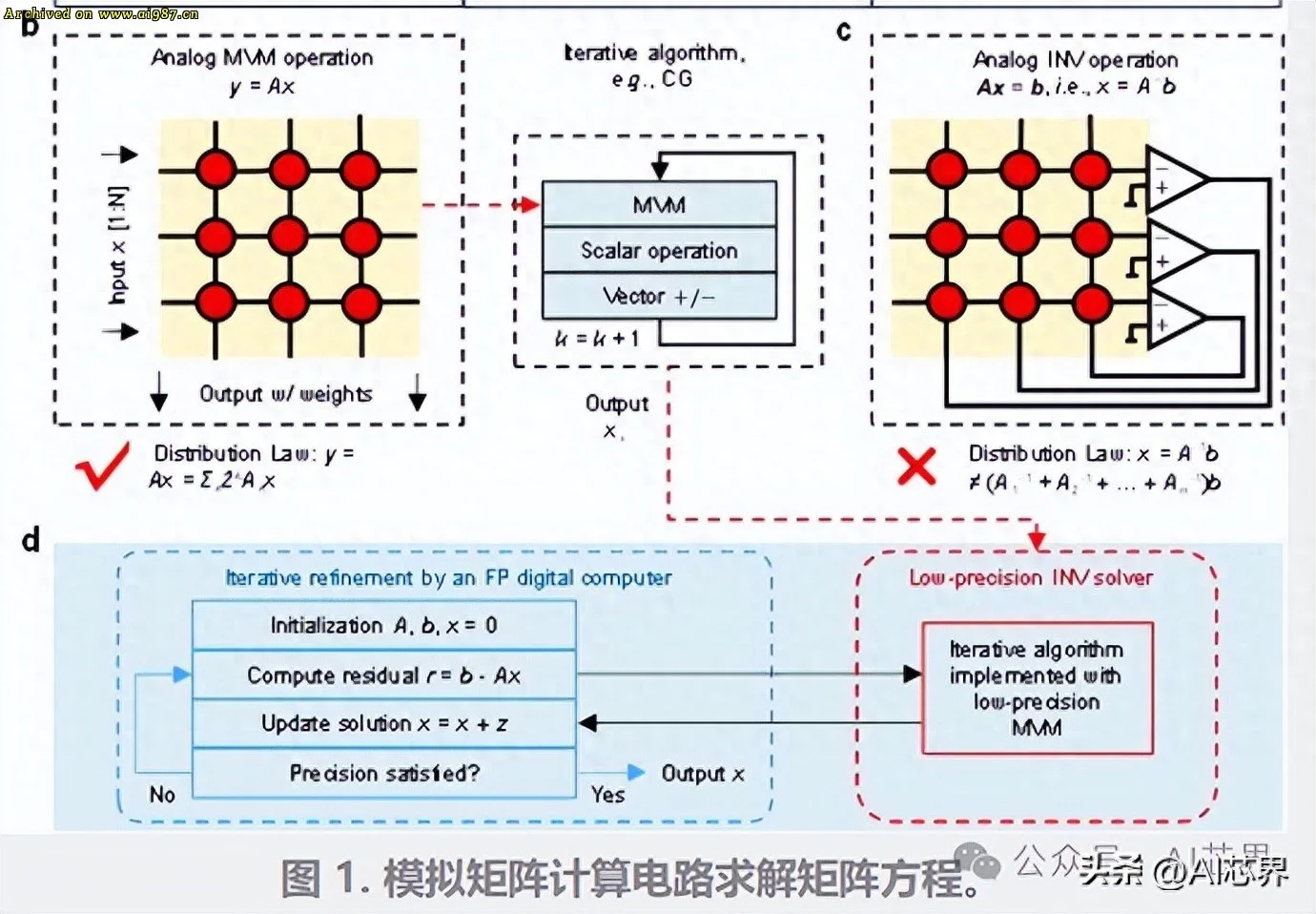
传统模拟计算的困境，北大融合创新构建了一个基于阻变存储器阵列的高精度、可拓展的全模拟矩阵方程求解器。新型信息器件、原创电路和经典算法协同设计的智慧结晶。

在高精度模拟矩阵求逆方面，研究团队基于迭代算法，巧妙地结合了模拟低精度矩阵求逆和模拟高精度矩阵 – 向量乘法运算。模拟低精度矩阵求逆和模拟高精度矩阵 – 向量乘法运算保留了模拟矩阵计算固有的低复杂度优势。其中，模拟矩阵求逆犹如一位经验丰富的领航员，能够在每次迭代中提供近似正确的结果，从而有效减少迭代次数。而高精度模拟矩阵 – 向量乘法（MVM）则通过位切片方法，实现了迭代细化过程，如同一位精细的雕刻师，逐步将计算精度提升至24位定点精度。

可扩展性设计是该架构的又一亮点。研究团队提出了块矩阵模拟计算方法，将复杂的矩阵计算问题像拼图一样分解到多个芯片上协同解决。使得大规模矩阵计算成为可能。在实验中，团队成功实现了16×16矩阵的24位特定点数精度求逆，为后续更大规模的计算任务奠定了坚实基础。

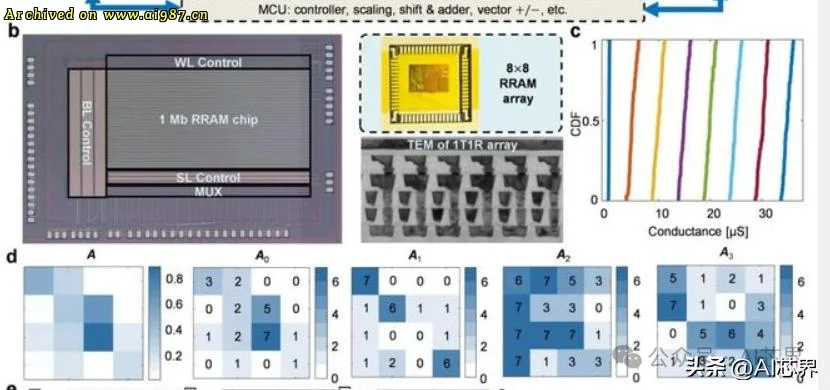
在硬件实现方面，模拟低精度矩阵求逆和模拟高精度矩阵 – 向量乘法运算两个电路的阻变存储器阵列在40nm CMOS工艺平台制造，可实现3比特电导态编程。这种硬件设计不仅保证了芯片的高性能，为后续的优化和升级提供方便。

三、爆炸性能

经过精心设计和实验验证，这款基于阻变存储器的模拟矩阵计算芯片展现出了卓越的性能。在计算精度方面，矩阵方程求解经过10次迭代后，相对误差可低至10⁻⁷量级，在模拟计算领域是一个前所未有的突破。

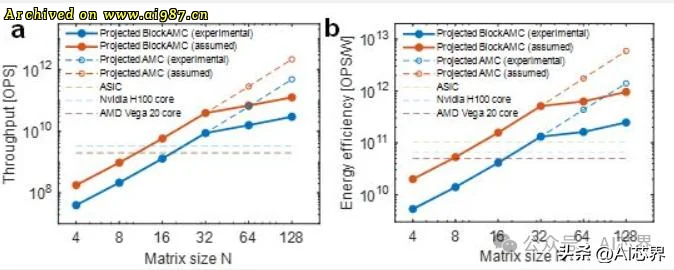
在计算性能上，在求解32×32矩阵求逆问题时，其算力已超越高端GPU的单核性能。当问题规模扩大至128×128时，计算吞吐量更达到顶级GPU的1000倍以上。这意味着传统GPU需要花费一整天时间才能完成的计算任务，这款芯片仅需一分钟就能轻松搞定。

在能效比方面，该方案在相同精度下能效比传统GPU提升超100倍，为高能效计算中心提供了关键技术支撑。这一优势在电力不足的今天，相比是多么雪中送炭。

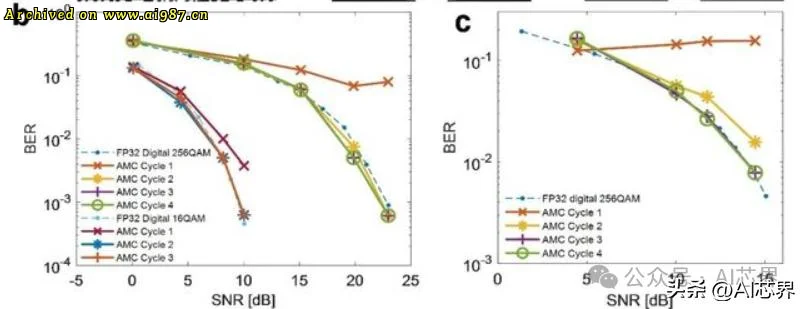
在应用验证方面，该方法被成功应用于大规模多输入多输出（MIMO）系统的信号检测任务。研究团队展示了基于迫零检测的图像恢复效果，在第二个迭代周期内，接收图像即与原始图像达到高度一致。进一步的误码率 – 信噪比分析显示，仅需三次迭代，该系统在无线通信场景下的检测性能即可媲美32位浮点精度GPU。

这项重大突破，在AI算力方面加速大模型训练中计算密集的二阶优化算法，显著提升训练效率。在边缘计算领域，低功耗特性将强力支持复杂信号处理和AI训推一体在终端设备上的直接运行，大大降低对云端的依赖，也推动边缘计算大力发展。

出处：头条号 @AI芯界